Des énigmes pour s’initier à la cryptographie
La cryptographie permet à sa manière de mettre les maths en scène. Source d’inspiration pour deux enseignants, elle les a amenés à imaginer tout un panel d’énigmes à résoudre dès l’école primaire et jusqu’à l’âge de la retraite. Cet article vous en présente certaines, réalisables sans ordinateur, mais aussi quelques pistes pour les mettre en œuvre avec vos élèves ou pour vous aider à les résoudre ! À vos crayons !
Pascal Lafourcade & Malika More
© APMEP Juin 2021
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Enseigner la cryptographie moderne n’est pas une chose facile. Les concepts mathématiques mis en jeu sont complexes et nécessitent souvent un niveau licence ou master pour les aborder. À première vue, il semble donc que cette science soit hors de portée d’écoliers, de collégiens ou de lycéens. Cependant, sont-ce les fondements théoriques et les preuves mathématiques sous-jacentes qui sont les plus importants pour de jeunes élèves ? Nous avons constaté que l’aspect enquête et défi de nos « missions cryptographiques » est pour eux une importante source de motivation. C’est pourquoi nous avons choisi de créer des énigmes que les élèves tenteront de comprendre pour leur faire découvrir par eux-mêmes certains principes de la cryptographie.
Quelques exemples d’énigmes
Du code PIN au code téléphone en passant par les codes correcteurs ou le code Morse, les codes et les chiffrements sont partout autour de nous !
Que ce soit à partir de bandelettes (figure 1), de permutations, de transpositions, de chiffrements homomorphes, de RSA ![]() , ou encore de l’usage du bibi-binaire1, il existe une multitude de techniques que nous vous invitons à découvrir au travers de plusieurs « Missions Cryptographiques » regroupant plus d’une cinquantaine d’énigmes, écrites sous forme de lettres manuscrites laissées par l’Agent0111. Pour rendre la recherche plus attractive, vous devrez découvrir des mots de passe permettant de passer d’une lettre à la suivante.
, ou encore de l’usage du bibi-binaire1, il existe une multitude de techniques que nous vous invitons à découvrir au travers de plusieurs « Missions Cryptographiques » regroupant plus d’une cinquantaine d’énigmes, écrites sous forme de lettres manuscrites laissées par l’Agent0111. Pour rendre la recherche plus attractive, vous devrez découvrir des mots de passe permettant de passer d’une lettre à la suivante.
| À qui de droit, |
| Reconstruisez le texte grâce aux dix bandelettes pour découvrir les coordonnées du point sur la dernière ligne. |
 |
| Agent0111 |
Sans vous en rendre compte, vous développerez votre connaissance des grands personnages ayant permis les plus grandes avancées en matière de cryptographie : du partage de secret de Shamir au chiffrement de Vigenère ou de Vernam en passant par le carré de Polybe, à Alberti (figure 2) ou encore à Mary Stuart, etc.
| À qui de droit, |
| Grâce au cadran d’Alberti vous allez déchiffrer le message suivant : IMPXHRNZSQ. |
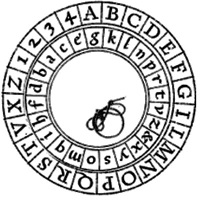 |
| Pour chiffrer, le disque est initialement mis dans cette position. Pour chaque lettre du message clair, la lettre du message chiffré est la lettre correspondante sur le disque intérieur. Tous les quatre caractères, le disque intérieur est tourné dans le sens inverse des aiguilles d’une montre de un secteur, ce qui a pour effet de modifier l’alphabet de substitution. Déchiffrer ce message vous permettra de trouver le mot de passe pour la prochaine lettre. |
| Agent0111 |
À travers ces énigmes, vous en prendrez plein la vue lors du déchiffrement des hommes dansants (figure 6), de l’utilisation de la scytale, de la compréhension de la stéganographie (figure 3) ou de la cryptographie visuelle. Découvrir le fonctionnement du Bitcoin, la première cryptomonnaie décentralisée inventée en 2009 par Satoshi Nakamoto, pourra également vous intéresser.
| À qui de droit, |
 |
| Un mot de passe est caché dans cette image, saurez-vous le trouver? Il est écrit en binaire mais vous devez le convertir en base 10 pour continuer la mission. |
| Agent0111 |
Apprendre la science informatique sans ordinateur et en s’amusant
Nous sommes convaincus que certains concepts fondamentaux de la science informatique peuvent être enseignés en partie grâce à des activités sans ordinateur, permettant découverte, réflexion et prise de recul, d’une manière complémentaire de celles qui se déroulent sur des machines. Cette drôle d’idée a été introduite par Tim Bell de l’Université de Canterbury ![]() dans les années 2000. Dans cette démarche, les activités se doivent de donner l’occasion aux élèves de se concentrer sur les concepts sous-jacents et les fondements de cette jeune science, à l’échelle de l’humanité, qu’est l’informatique, sans être distraits par les facilités et les difficultés liées à l’utilisation de l’objet technologique qu’est l’ordinateur.
dans les années 2000. Dans cette démarche, les activités se doivent de donner l’occasion aux élèves de se concentrer sur les concepts sous-jacents et les fondements de cette jeune science, à l’échelle de l’humanité, qu’est l’informatique, sans être distraits par les facilités et les difficultés liées à l’utilisation de l’objet technologique qu’est l’ordinateur.
Rappelons que l’ordinateur a d’abord été théoriquement conçu en 1936 par Alan Turing, le père de l’informatique, avant de ne devenir réalité que quelques années plus tard, grâce aux progrès de la physique et de l’électronique. Cette invention de moins de cent ans est aujourd’hui omniprésente dans nos vies et a radicalement changé notre façon d’appréhender le monde et la connaissance. Il nous semble donc essentiel de nous appliquer à enseigner de toutes les façons possibles les concepts qui ont permis cette révolution numérique. Dans cet esprit, toutes les énigmes de cryptographie que nous proposons sont réalisables à l’aide d’un papier, d’un crayon, et surtout d’une bonne dose de curiosité et de réflexion.
En effet, dans l’apprentissage, il est bien entendu essentiel de susciter la curiosité des élèves et de les rendre acteurs. C’est pour cela qu’au lieu de proposer un cours et des exercices, nous avons préféré concevoir des énigmes, que les élèves doivent résoudre seuls, les unes après les autres, pour qu’ils découvrent par eux-mêmes les concepts impliqués. À chaque étape, pour parvenir à percer le secret, ils doivent faire preuve de créativité et solliciter leurs connaissances.
Construire une mission cryptographique
Chaque énigme est conçue autour d’une avancée majeure en matière de cryptographie ou de sécurité informatique. Autrement dit, chacune des énigmes a été élaborée dans le but de faire découvrir un concept important de ce domaine. La « mise en énigme » du concept cryptographique est parfois simple et évidente, mais demande parfois une longue réflexion et de nombreux essais avant de trouver la formulation adaptée.
La première étape de création d’une énigme est de choisir le concept qu’elle devra illustrer. De plus, il faut surtout veiller à donner assez d’indices pour que l’élève puisse avancer par lui-même en faisant appel à son sens de l’observation, sa créativité et son esprit de déduction. Pour l’énigme sur le chiffrement de César, le professeur peut faire remarquer qu’une lettre a une structure particulière ou encore proposer aux élèves de rechercher ce qu’est un pangramme2. Il est donc important d’adapter l’énoncé de l’énigme au public visé, en fonction de son âge, de ses compétences, du temps imparti, et du nombre d’élèves travaillant ensemble.
Par ailleurs, nous recommandons vivement de tester entièrement les énigmes avant de les proposer, car une erreur est vite arrivée et risque de démotiver totalement les participants, voire de rendre l’énigme impossible à résoudre. Cette tâche est souvent difficile pour le concepteur de l’énigme. C’est pourquoi nous vous encourageons à collaborer avec un ami, un collègue ou un jeune bêta-testeur, pour vous assurer que l’énigme est correctement rédigée, ne contient pas d’erreur et que la durée et la difficulté sont adaptées au public visé. Leur résolution ne requiert pas de matériel particulier (autre que papier, crayon, calculatrice éventuellement), mais il est préférable que chaque élève dispose d’une copie de l’énoncé de l’énigme. Il est aussi souhaitable de faire travailler les élèves par groupes de \(3\) à \(5\), pour créer une émulation et stimuler la créativité. L’aspect challenge et compétition, qui s’instaure rapidement, fait partie de ce que les participants disent souvent après coup avoir beaucoup apprécié dans les missions cryptographiques.
Ces missions ont été conçues de manière à être adaptées à différents publics et pour différentes occasions. Par exemple, le chiffrement de César est une substitution mono-alphabétique : il s’agit de remplacer chaque lettre du message en clair par celle qui se trouve décalée de trois rangs vers la droite dans l’alphabet. À titre d’échauffement historique, une des premières énigmes de chaque mission cryptographique se compose de deux messages, l’un en clair (figure 4) et l’autre chiffré à l’aide du chiffrement de César (figure 5).
| À qui de droit, |
| Si vous lisez cette lettre, c’est que mes ennemis m’auront retrouvé et que j’ai dû fuir. Rassurez-vous, j’ai laissé des indications et le mot de passe pour ouvrir mon coffre plein de trésors se révélera à ceux qui seront assez persévérants. Cela ne sera pas simple, j’ai utilisé tous mes codes secrets afin d’égarer les curieux et mes~ennemis. Bonne chance! |
| Post-Scriptum: Décryptez-moi ces jeux bien plus vite que Sherlock et Watson pour finir et~gagner! |
| Agent0111 |
L’énigme consiste à décrypter le second message (figure 5), bien entendu sans connaître la méthode de chiffrement utilisée.
| D txl gh gurlw, |
| Mh yrlv txh yrxv dyhc frpsulv oh irqfwlrqqhphqw gx frgh gh FHVDU, txl frqvlvwh d ghfdohu fkdtxh ohwwuh gh wurlv srvlwlrqv yhuv od gurlwh gdqv o doskdehw.Uhwhqhc fh suhplhu srlqw vhfuhw g devflvvh prlqv flqt hw g rugrqqhh prlqv ylqjw wurlv. |
| Djhqw0111 |
| Srvw-Vfulswxp: Ghfubswhc prl fhv mhxa elhq soxv ylwh txh Vkhuorfn hw
Zdwvrq srxu ilqlu hw jdjqhu! Srvw-Vfulswxp 2: Uhwurxyhc ohv wurlv prwv gh sdvvh d sduwlu gx ilfklhu gh prwv gh sdvvh (ohwwuh ghxa). |
Cette approche met l’élève face à un défi de difficulté raisonnable, lui demandant de découvrir par lui-même comment ce texte a été chiffré. Il peut d’abord remarquer qu’il y a des points communs dans la mise en page, et que le message chiffré est par conséquent lui aussi probablement une lettre. Par exemple, la phrase de début semble être à la même place, il est donc fort probable que le message « À qui de droit » soit chiffré par « D txl gh gurlw » . Les élèves remarquent en général cela sans aide, et en déduisent que chaque lettre de l’alphabet a été remplacée par une autre. Pour aider les plus jeunes à y penser, il est possible de leur distribuer un tableau comprenant sur une ligne les lettres de l’alphabet, et une ligne de cases vides en dessous :
| Clair | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| Chiffré |
La correspondance des lettres suivantes est obtenue en observant la phrase d’introduction :
| Clair | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| Chiffré | d | g | h | l | r | t | u | w | x |
Il y a plusieurs façons de continuer à résoudre cette énigme :
- remplacer les lettres trouvées dans le message chiffré et deviner les mots manquants pour compléter le tableau ;
- remarquer une logique dans les lettres trouvées et s’apercevoir qu’il y a un décalage de trois lettres dans l’alphabet ;
- continuer à observer les messages et remarquer que le post-scriptum est un pangramme permettant de trouver rapidement toutes les lettres de l’alphabet.
Cette énigme sur le chiffrement de César a été testée dès la classe de CM2, en proposant un message chiffré plus court que celui de la figure 5, jusqu’au grand public, en passant par des étudiants en DUT d’informatique.
Depuis plusieurs années, nous avons testé nos énigmes dans différents cadres.
Chaque fois, nous avons sélectionné quelques énigmes et adapté les énoncés au niveau des participants et au temps dont ils disposaient. Par exemple nous avons proposé les dancing men à des collégiens (il s’agit d’une substitution, comme le chiffrement de César, mais où les lettres de l’alphabet sont remplacées par des dessins de bonshommes qui semblent danser, voir figure 6).

Pour introduire le concept de partage de secret, inventé par Adi Shamir, à des lycéens, chaque groupe d’élève doit déterminer, en résolvant les énigmes précédentes, les coordonnées d’un point du plan. Ensuite, trois groupes doivent mettre en commun les valeurs qu’ils ont trouvées, et résoudre un système linéaire pour trouver l’équation d’une parabole, dont l’ordonnée à l’origine est la réponse à l’énigme.
Afin de proposer ce concept pour des élèves de CM2-6 nous avons utilisé une variante beaucoup plus simple. Dans ce cas, à partir des nombres secrets découverts dans les énigmes précédentes, nous avons simplement demandé aux jeunes élèves d’additionner trois de ces nombres, puis de calculer le reste d’une certaine division du résultat, pour trouver le code du cadenas du coffre à bonbons. Ces types d’adaptations, parfois radicales, sont indispensables pour la motivation des participants.
Animer une mission cryptographique
Les énigmes sont conçues pour un travail autonome des élèves. C’est pourquoi il nous semble préférable que le rôle de l’enseignant se limite à accompagner l’élève dans sa recherche, à son propre rythme. Il n’intervient que si nécessaire, pour guider avec parcimonie les élèves dans la compréhension et la découverte de la solution de l’énigme. Il doit principalement veiller à ce que les élèves ne partent pas trop loin et ne cherchent pas des choses trop complexes. Il peut aussi donner, si besoin, quelques indices supplémentaires pour les mettre sur la voie. Par exemple l’énigme de la figure 7 est très difficile sans indices, mais peut se faire simplement avec des élèves de primaire si l’enseignant les aide à exploiter le code RGB (Red, Green, Blue), en leur expliquant comment sont codés les pixels en informatique à l’aide des trois couleurs rouge, vert et bleu.
| À qui de droit, |
| À qui de droit, J’ai intercepté un message contenant les nombres suivants. Il y a exactement \(3\times23\times17\) nombres. Saurez-vous, comme moi, voir qui a écrit ce message ? |
 |
| Agent0111 |
Ainsi en remarquant que le rouge est codé par (\(255\), \(000\), \(000\)), le bleu par (\(000\), \(000\), \(255\)) et le jaune par (\(255\), \(255\), \(000\)), il est possible de découvrir l’image d’un super-héros qui porte ces couleurs.
Il est donc important que l’enseignant se contente d’observer les élèves chercher au premier abord, qu’il n’intervienne pas trop vite, et bien entendu qu’il ne résolve surtout pas les énigmes à leur place.
En revanche, l’enseignant reprend la main, une fois l’énigme ou la série d’énigmes terminée, pour expliciter ce que les élèves ont découvert. Pour cela, il formalise leurs découvertes avec les mots et les concepts correspondants, leur fait décrire comment ils ont fait, ce qui était difficile et comment ils ont surmonté ces défis.
Toutes les énigmes que nous avons créées sont rassemblées dans plusieurs « Missions Cryptographiques » et sont librement accessibles 24 h/24 sur le site web ![]() .
.
Il est donc possible à chacun de se lancer dans leur résolution à tout moment. Cependant, afin de permettre aux auteurs de dormir un peu, la version en ligne de chaque énigme consiste à découvrir un nom d’utilisateur (login) et un mot de passe permettant de passer à la suivante. Cette idée s’inspire du principe d’un jeu en ligne addictif, Ouverture facile ![]() . Attention, les mots de passe et les noms d’utilisateur doivent respecter les minuscules/majuscules et sont donc sensibles à la casse. Ce mécanisme, qui techniquement utilise un simple fichier
. Attention, les mots de passe et les noms d’utilisateur doivent respecter les minuscules/majuscules et sont donc sensibles à la casse. Ce mécanisme, qui techniquement utilise un simple fichier .htaccess, permet de vérifier que l’investigateur a correctement résolu chaque énigme avant de passer à la suivante. Cela permet aussi de concevoir une progression dans les énigmes et de choisir l’ordre dans lequel elles sont présentées. Cependant, sur le site, la difficulté des énigmes n’est absolument pas croissante, mais dépend uniquement de l’inspiration du moment de l’auteur.
Conclusion
Finalement, nous présentons, à travers ces énigmes, une manière ludique d’initier les élèves à des concepts fondamentaux de cryptographie et de sécurité informatique. Nous espérons avoir montré la flexibilité de cette proposition. Nous encourageons les collègues enseignants à s’en saisir, pour adapter leurs énigmes préférées au niveau de leurs élèves, au temps dont ils disposent et à la forme qu’ils souhaitent donner à « leur » mission cryptographique.
Nous serons heureux de répondre aux questions et de recevoir les retours de ceux qui voudront s’y essayer. C’est dans cette optique de pouvoir vous accompagner que nous avons écrit un ouvrage [1] , composé d’une sélection de vingt-cinq énigmes, avec trois niveaux d’indices permettant d’aider les lecteurs en difficulté, accompagnées de leurs solutions détaillées et de nombreux encarts historiques, culturels, biographiques, techniques et mathématiques, que nous vous invitons à découvrir.
Références
- [1] Pascal Lafourcade et Malika More, 25 énigmes ludiques pour s’initier à la cryptographie. 1re édition. Dunod, 5 mai 2021.↩
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
Pascal Lafourcade est maître de conférence à l’Université Clermont-Auvergne et membre du LIMOS3
.
Malika More est maîtresse de conférences à l’IUT d’informatique de l’Université Clermont-Auvergne et membre du LIMOS .
- Système de notation de la base16, inventé par le chanteur Boby Lapointe, utilisant les syllabes ho, ha, he, hi, bo, ba, be, bi, ko, ka, ke, ki, do, da, de et di. ↩
- Un pangramme est une phrase qui contient toutes les lettres de l’alphabet.↩
- Laboratoire d’Informatique, Modélisation et Optimisation des Systèmes.↩

